개별 트리 모델의 단점
- 계층적 구조로 인해 중간에 에러가 발생하면 다음 단계로 에러가 계속 전파
- 학습 데이터의 미세한 변동에도 최종 결과 크게 영향
- 적은 개수의 노이즈에도 크게 영향
- 나무의 최종노드 개수를 늘리면 과적합 위험 (Low bias, Large Variance)
- 해결 방안으로, Random Forest가 있음
앙상블 (랜덤 포레스트의 배경)
- 여러 Base 모델들의 예측을 다수결 법칙 또는 평균을 이용해 통합하여 예측 정확성을 향상시키는 방법

- 다음 조건을 만족할 때 앙상블 모델은 Base 모델보다 우수한 성능을 보여줌
- Base 모델들이 서로 독립적
- Base 모델들이 무작위 예측을 수행하는 모델보다 성능이 좋은 경우
ex) 5개의 binary classifier를 base 모델로 가지는 앙상블 모델의 오류율은 아래 그림과 같이 나타남. Base 모델의
성능이 무작위 모델보다는 좋아야 함
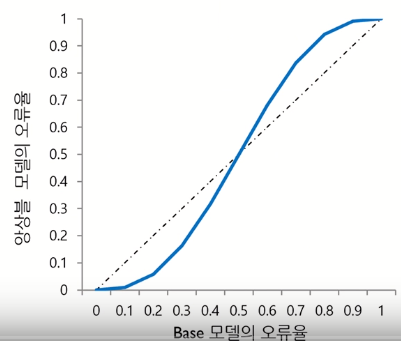
- 의사결정나무모델은 앙상블 모델의 base 모델로써 활용도가 높음
- Low computational complexity : 데이터의 크기가 방대한 경우에도 모델을 빨리 구축할 수 있음
- Non-parametric : 데이터 분포에 대한 전제가 필요하지 않음
랜덤 포레스트 개요
- 다수의 의사결정나무모델에 의한 예측을 종합하는 앙상블 방법
- 일반적으로 하나의 의사결정나무모델 보다 높은 예측 정확성을 보여줌
- 관측치 수에 비해 변수의 수가 많은 고차원 데이터에서 중요 변수 선택 기법으로 널리 활용됨
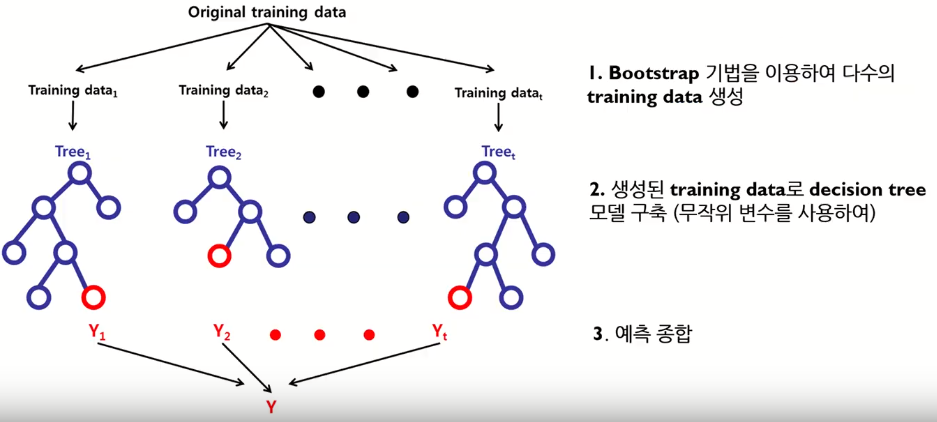
핵심 아이디어 : Diversity, Random 확보
- 여러 개의 training data를 생성하여 각 데이터마다 개별 의사결정나무모델 구축 → Bagging
- 의사결정나무모델 구축 시 변수 무작위로 선택 → Random subspace
앙상블 모델의 성능이 좋기 위한 전제 조건이, diversity와 randomness를 확보하는 것이다.
각각의 모델이 bootstrap으로 diversity를 확보하고.. random subspace로 분기를 나누면서 randomness를 확보하는 것.
- diversity를 확보하면서 각 모델을 이용하여 다양한 방면의 정보를 획득할 수 있을 것 (앙상블 모델은 각 base 모델이 독립적이어야 좋은데, 그러한 부분을 어느정도 보장하는 것)
- randomness를 확보함으로써 모델의 variance를 줄여줄 수 있을 것 같음 (변수 많이 select하면, 당연히 복잡도 높아져서 variance 또한 클 것. 일반화 성능을 높이는 효과)
- bagging과 random subspace 기법은 각 모델들의 독립성, 일반화, 무작위성을 최대화 시켜 모델간의 상관관계 a를 감소시킴
- RF는 어떤 확률분포를 가정하지 않기 때문에, 비모수적(Non-parametric) 모델임
Bagging (Bootstrap Aggregating)
- 각각의 bootstrap 샘플로부터 생성된 모델을 합침
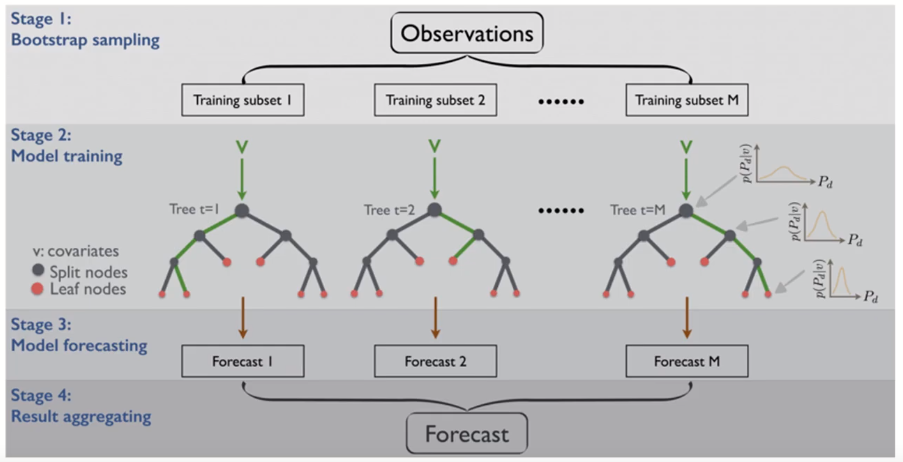
- Bootstrapping ( → sampling)
- 각 모델은 서로 다른 학습 데이터셋을 이용
- 각 데이터셋은 복원 추출(sampling with replacement)을 통해 원래 데이터의 수 만큼의 크기를 갖도록 샘플링
- 개별 데이터셋을 bootstrap set이라 부름
- Result Aggregating
- For classification problem
- Majority voting
- Weighted voting (weight = training accuracy of individual models)
- Weighted voting (weight = predicted probability for each class)
- Bagging: algorithm

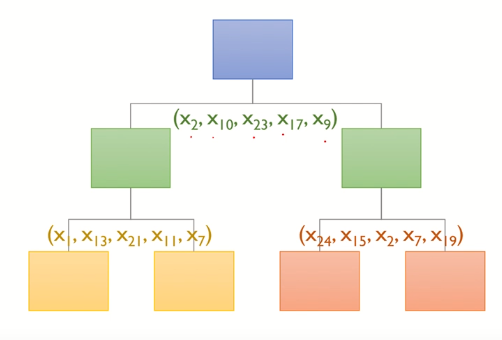
Random Subspace
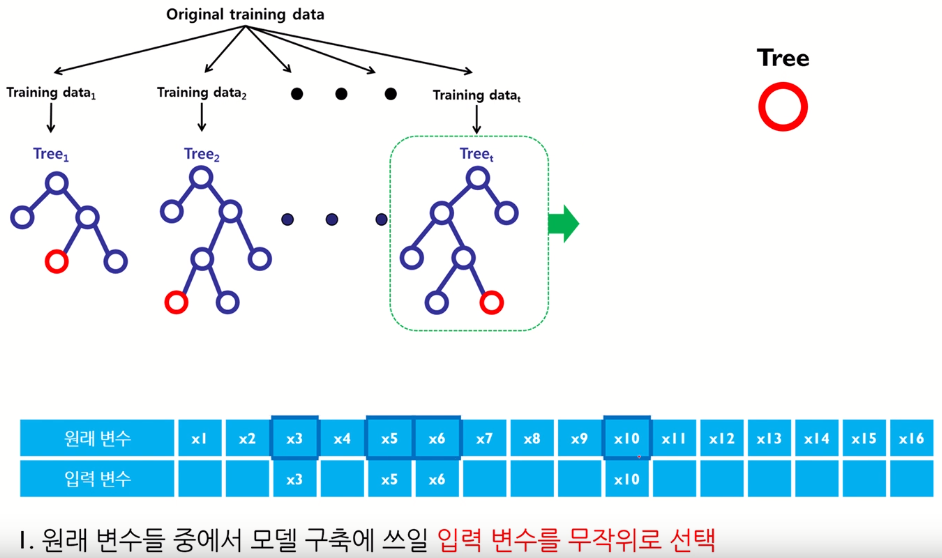


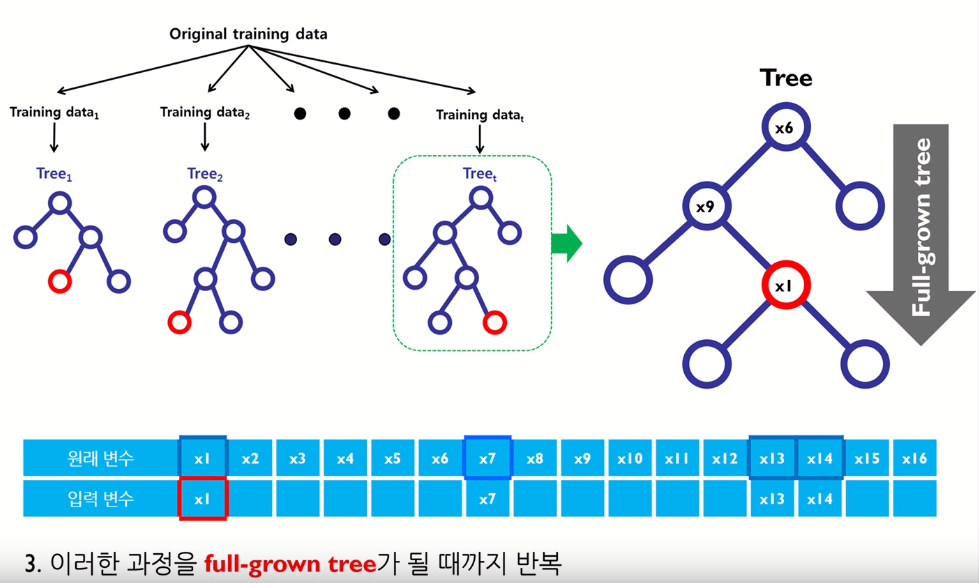
- 즉, 의사결정나무의 분기점을 탐색할 때, 원래 변수의 수보다 적은 수의 변수를 임의로 선택하여 해당 변수들만을 고려대상으로 함
Generalization Error
- 각각의 개별 tree는 과적합될 수 있음
- Random forest는 tree 수가 충분히 많을 때 Strong Law of Large Numbers에 의해 과적합 되지 않고 그 에러는
limiting value에 수렴됨

- 개별 tree의 정확도가 높을수록 s 증가
- Bagging과 random subspace 기법은 각 모델들의 독립성, 일반화, 무작위성을 최대화시켜 모델간의 상관관계 ρ 를
감소시킴
- 개별 tree의 정확도, 독립성이 높을수록 random forest의 성능이 높아짐
중요 변수 선택
- 변수의 중요도
- 랜덤 포레스트는 선형 회귀모델/로지스틱 회귀모델과는 달리 개별 변수가 통계적으로 얼마나 유의한지에 대한 정보를 제공하지 않음 (∵ 확률분포를 가정하지 않음 (선형회귀는 error가 정규분포임을 가정))
- 대신 랜덤 포레스트는 다음과 같은 간접적인 방식으로 변수의 중요도를 결정
1단계 : 원래 데이터 집합에 대해서 Out of bag(OOB) error를 구함
2단계 : 특정 변수의 값을 임의로 뒤섞은 데이터 집합에 대해서 OOB error를 구함
3단계 : 개별 변수의 중요도는 2단계와 1단계 OOB error 차이의 평균과 분산을 고려하여 결정
- Out of bag (OOB) → About 33% of original data are not selected in bootstrap
- Used for out-of-bag error and variable importance
- Bagging을 사용할 경우 bootstrap set에 포함되지 않는 데이터들을 검증 집합으로 사용함

- 중요 변수 선택
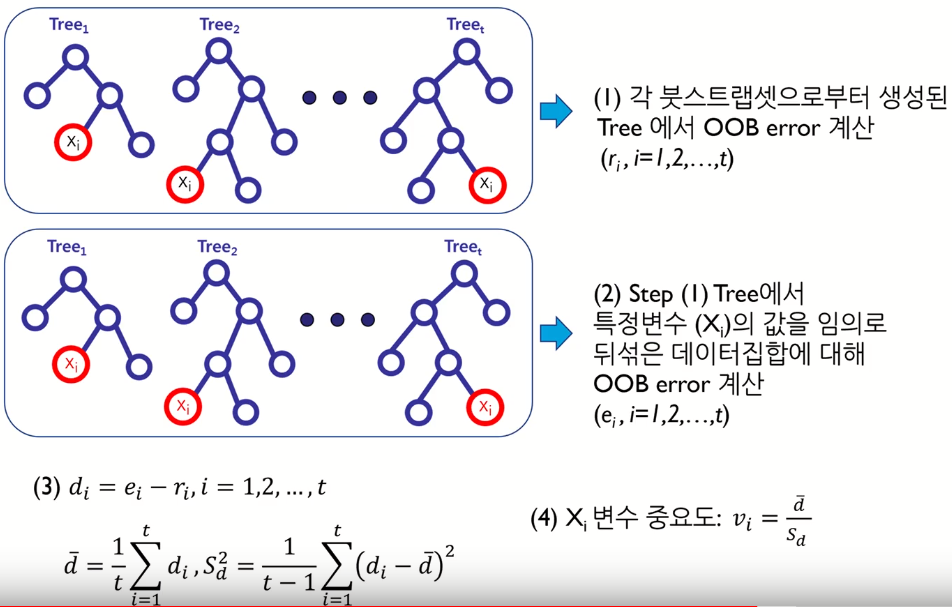
(4) 에서 sd 나눠주는 것은 scaling의 역할. 변동이 너무 큰 경우에 평균이 높더라도 중요도 좀 낮춰주기 위해.
하이퍼 파라미터
- Decision tree의 수 (n_estimators)
- Strong law of large numbers 을 만족시키기 위해 2,000개 이상의 decision tree 필요
(그러나, 아닌 경우도 많이 있음. search 및 최적화가 필요) (default 값이 대부분 10) - Decision tree에서 노드 분할 시 무작위로 선택되는 변수의 수 (Max_features)
- 일반적으로 변수의 수에 따라 다음과 같이 추천됨 (Diaz-Uriarte et el., 2006) (그러나, guide line일 뿐 search 필요)
- 이 값이 크면 performance가 향상될 수 있지만, overfitting의 가능성 존재
- Classification : sqrt(변수의 수)
- Regression : 변수의 수/3
- 옵션 : auto(제한 없음), sqrt(전체 feature 갯수에 square root), log2 (전체 feature 갯수에 log2) - Max_depth
- 각 트리의 최대 depth를 의미함
- Default 값은 대부분 None. 즉, 모든 leaf가 pure해질 때 까지 트리를 만드는 것.
(Pure하다는 것은, 하나의 leaf에 해당하는 데이터가 동일한 class를 가지는 상태임) - Min_sample_leaf
- 각 leaf 노드에서의 최소 데이터 갯수
- Default 값은 대부분 1. 즉, 모든 leaf 노드는 1개 이상의 데이터를 가져야 함
- 특히 regression 문제에서, smoothing 효과와 관련 있음
- Training dataset의 갯수를 보고 결정해야 함 - Min_sample_split- Leaf 가 아닌 노드(internal node)에서의 최소 데이터 갯수
- Default 값은 대부분 2. 즉, split 되기 전의 internal node는 2개 이상의 데이터를 가져야 함
- 값이 너무 크면 underfitting 가능성 있음
- Training dataset의 갯수를 보고 결정해야 함
Cross-validation 과 random search를 통해 (1, 3, 4, 5) 혹은 (1, 3, 4) 최적화 할 수 있다.
Aggregate 방법의 경우, classification이면 voting, regression이면 average가 default로 결정되어 있음


랜덤 포레스트 알고리즘

Advantages
- Overall
- For many data sets, it produces a highly accurate classifier (Almost same as SVMs and NNs)
- It is faster to train and has fewer parameters than SVMs and NNs (good for large databases)
- It is interpretable
- Training
- It generates an internal unbiased estimate of the generalization error (Cross validation is unnecessary) (∵ OOB error)
- Resistance to over training
- Data
- Ability to handle data without preprocessing
- Data does not need to be rescaled, transformed, or modified
- Resistant to outliers
- It can handle thousands of input variables without variable deletion (Good for problems where k>>N)
[참조]
김성범 교수님의 https://www.youtube.com/watch?v=lIT5-piVtRw (랜덤포레스트 모델) 을 요약한 것입니다.
https://towardsdatascience.com/optimizing-hyperparameters-in-random-forest-classification-ec7741f9d3f6 (Hyper-parameter)
https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html (Hyper-parameter)
https://medium.com/@ODSC/optimizing-hyperparameters-for-random-forest-algorithms-in-scikit-learn-d60b7aa07ead (Hyper-parameter)
'Machine Learning > Algorithm' 카테고리의 다른 글
| Linear Regression (선형회귀모델) - 1 (개요, 가정) (0) | 2019.10.13 |
|---|---|
| Local Outlier Factors (LOF) (0) | 2019.10.07 |
| Outlier Detection (standard deviation v.s. interquartile range) (0) | 2019.08.21 |
| DBSCAN (0) | 2019.08.18 |
| Singular Value Decomposition (SVD) (0) | 2019.08.18 |