- 결정계수 (Coefficient of Determination: $R^{2}$)
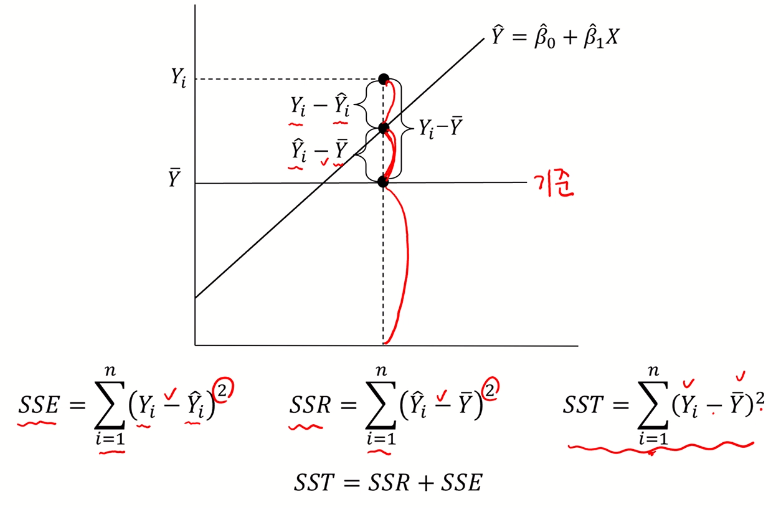
- $\overline{Y}$ : 그냥 Y값만을 이용하여 설명할 수 있는 정도 (baseline)
- SST : $\overline{Y}$로부터의 Y값 변동
- SSR : 갖고 있는 X를 이용하여 얼만큼 설명할 수 있는지
- SSE : X로 설명할 수 없는 부분
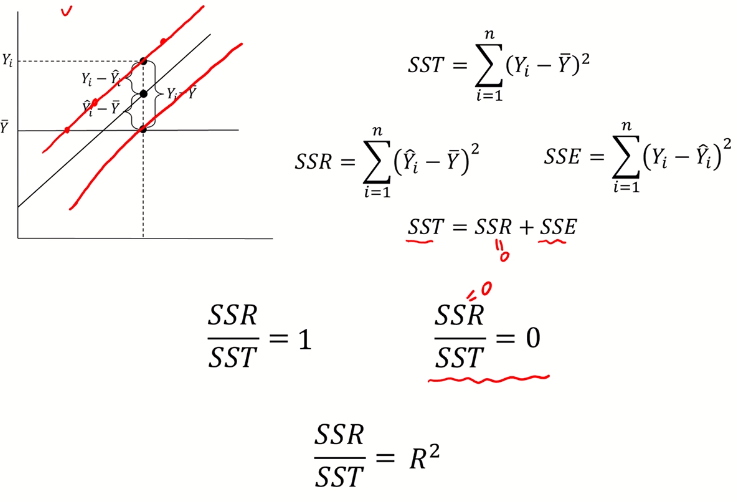
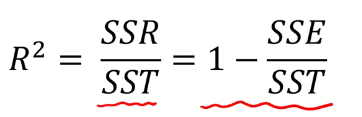
- $R^{2}$는 0과 1 사이에 존재
- $R^{2}=1$ : 현재 가지고 있는 X 변수로 Y를 100% 설명. 즉, 모든 관측치가 회귀직선 위에 있다.
- $R^{2}=0$ : 현재 가지고 있는 X 변수는 Y 설명(예측)에 전혀 도움이 되지 않는다.
- 사용하고 있는 X 변수가 Y 변수의 분산을 얼마나 줄였는지 정도
→ 1이면 100% 다 줄인 것
→ 0.2라면 20% 정도 줄인 것
- 단순히 Y의 평균값($\overline{Y}$)을 사용했을 때 대비 X 정보를 사용함으로써 얻는 성능 향상 정도
- 사용하고 있는 X 변수의 품질
- 수정 결정계수 (Adjusted $R^{2}$)
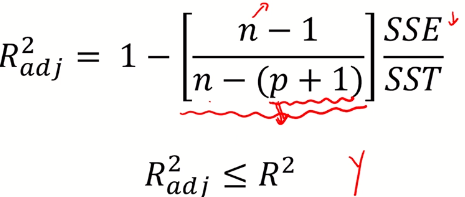
- $R^{2}$는 유의하지 않은 변수가 추가되어도 항상 증가
- 수정 $R^{2}$는 앞에 특정 계수를 곱해 줌으로써(보정) 유의하지 않은 변수가 추가될 경우 증가하지 않게 함
- 설명변수가 서로 다른 회귀모형의 설명력을 비교할 때 사용
- 선형회귀모델 예제


- 판매원 수와 광고비 변수에 의해 매출액 변수의 변동성을 68.3% 감소
- 매출액의 (단순)평균 대비 판매원 수와 광고비를 이용하면 설명력이 68.3% 증가
- 현재 분석에 사용하고 있는 판매원 수와 광고비의 "변수 품질" 정도가 68.3 (100점 기준)
- 선형회귀모델에서의 분산분석
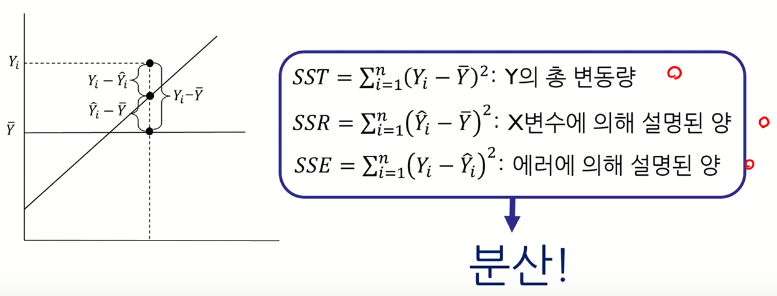
- 분산분석 : Analysis of Variance (ANOVA)
- 분산 정보를 이용하여 분석 (SST, SSR, SSE 모두 편차 제곱의 평균 처럼 분산이라고 할 수 있음)
- 분산분석은 궁극적으로 가설 검정을 행하는 용도로 사용
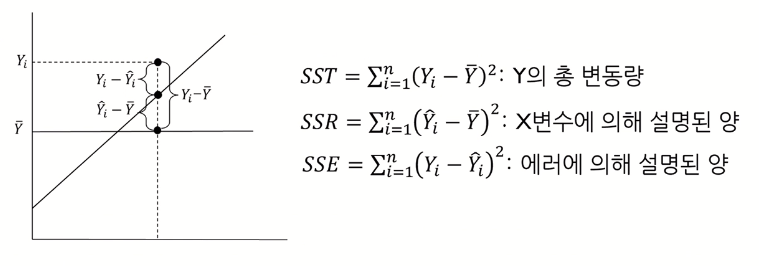
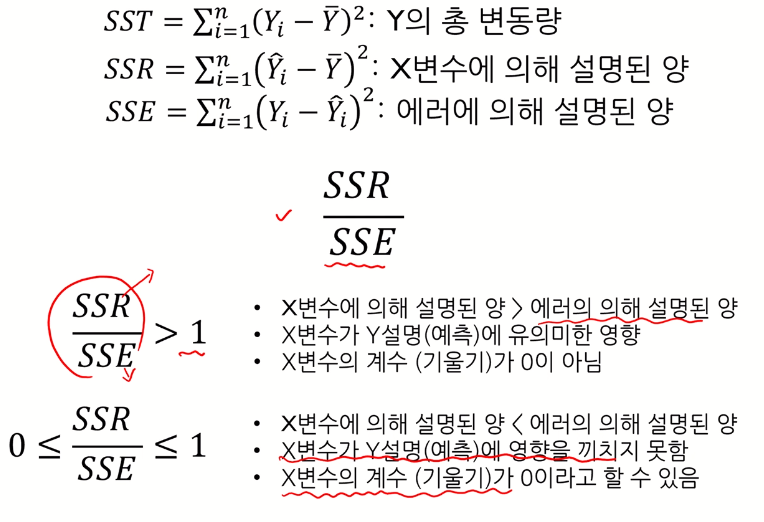
- 얼마나 커야 큰 값인지?
- 분포를 알면 통계적으로 판단할 수 있음
- 안타깝게도 직접적으로 분포를 정의할 수 없음
- 하지만, SSR과 SSE가 각각 카이제곱 분포 (파라미터 : 자유도)를 따름


- 지금까지 설명한 것들을 테이블로 정리해보자 (단순회귀모델의 경우)
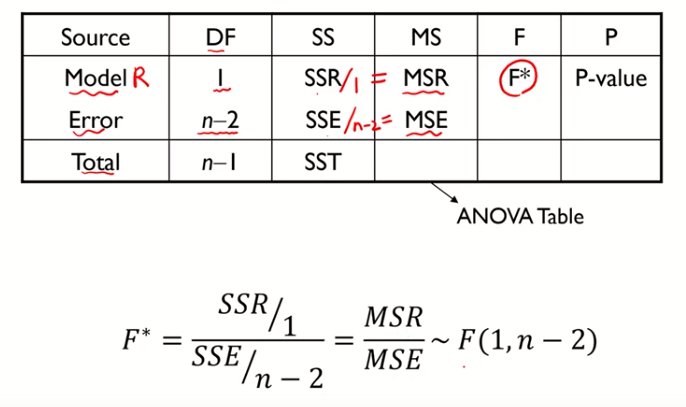
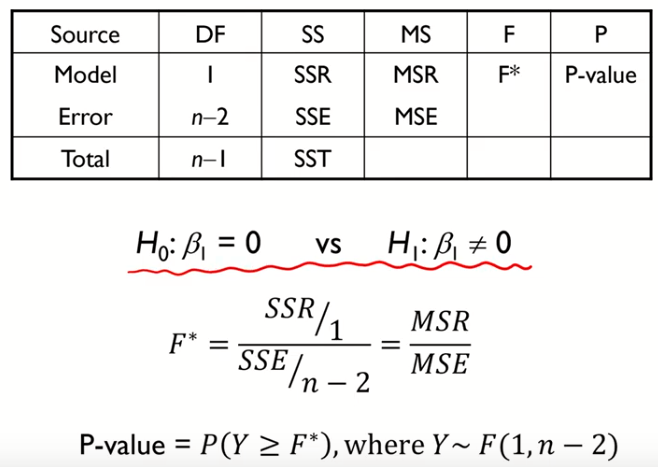
- P-value가 0과 가까우면, $F^{*}$ 값이 큰 것이고, 그러면 $\beta_{1}=0$ 이라는 귀무가설 기각한다.
- 선형회귀모델에서의 분산분석 예제

'Machine Learning > Algorithm' 카테고리의 다른 글
| Logistic regression (로지스틱 회귀모델) - 2 (학습, 해석) (0) | 2020.03.11 |
|---|---|
| Logistic regression (로지스틱 회귀모델) - 1 (배경, 형태, odds) (0) | 2020.03.05 |
| Linear Regression (선형회귀모델) - 3 (파라미터 구간 추정, 가설 검정) (0) | 2020.02.10 |
| PCA reconstruction for anomaly detection (0) | 2020.02.06 |
| Partial Least Squares (PLS) (0) | 2020.01.15 |