- 분류 및 예측을 위한 모델
- Model-based Learning
- 선형/비선형 모델(e.g., linear regression, logistic reegression)
- Neural network
- 의사 결정 나무
- Support vector machine
→ 데이터로부터 모델을 생성하여 분류/예측 진행
- Instance-based Learning
- K-nearest neighbor
- Locally weighted regression
→ 별도의 모델 생성 없이 인접 데이터를 분류/예측에 사용
- KNN 알고리즘의 구분 및 특징
- Instance-based Learning
- 각각의 관측치 (instance)만을 이용하여 새로운 데이터에 대한 예측을 진행
- Memory-based Learning
- 모든 학습 데이터를 메모리에 저장한 후, 이를 바탕으로 예측 시도
- Lazy Learning
- 모델을 별도로 학습하지 않는 테스팅 데이터가 들어와야 비로소 작동하는 게으른(lazy) 알고리즘
- 거리 측도 (1-유사도)
- 다양한 거리 측도(Distance measure) 존재 (e.g., Euclidean distance, Correlation distance, ...)
- 데이터 내 변수들이 각기 다른 데이터 범위, 분산 등을 가질 수 있으므로, 데이터 정규화(혹은 표준화)를 통해 이를 맞추는 것이 중요함
- 거리를 계산할 때, 단위가 큰 특정 변수(들)가 거리를 결정하는 것 방지
- 예) 키(1.5m~1.8m), 몸무게(90lb~300lb), 연봉(20,000,000원~100,000,000원)
- KNN의 장점과 한계점
- 장점
- 데이터 내 노이즈에 영향을 크게 받지 않으며, 특히 Mahalanobis distance와 같이 데이터의 분산을 고려할 경우
강건함
- 학습 데이터의 수가 많을 경우 효과적임
- 한계점
- 파라미터 k의 값을 설정해야 함
- 어떤 거리 척도가 분산에 적합한 지 불분명하며, 따라서 데이터의 특성에 맞는 거리 측도를 임의로 선정해야함
- 새로운 관측치와 각각의 학습 데이터 간 거리를 전부 측정해야 하므로, 계산시간이 오래 걸리는 단점이 있음
- Euclidean Distance

- 가장 흔히 사용하는 거리측도
- 대응되는 X, Y값 간 차이 제곱합의 제곱근으로써, 두 관측치 사이의 직선 거리를 의미함



- Manhattan Distance

- X에서 Y로 이동 시 각 좌표축 방향으로만 이동할 경우에 계산되는 거리

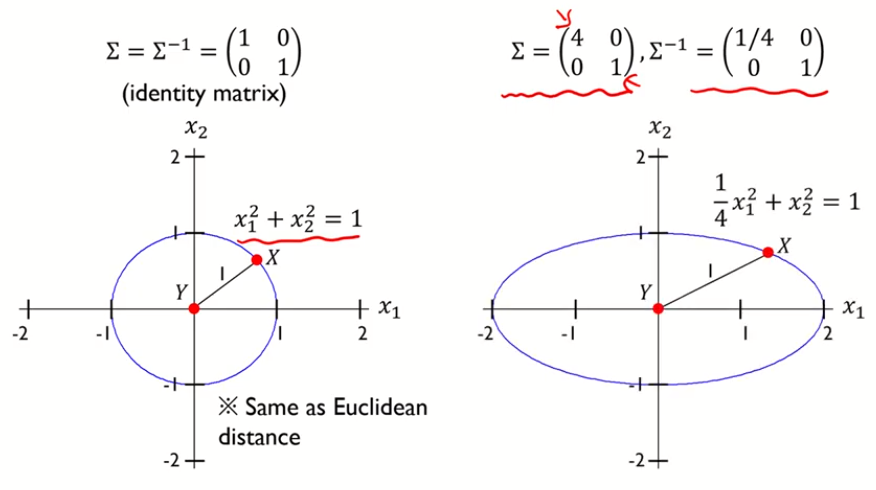
- Mahalanobis Distance

- 변수 내 분산, 변수 간 공분산을 모두 반영하여 X, Y간 거리를 계산하는 방식
- 데이터의 covariance matrix가 identity matrix인 경우는 Euclidean distance와 동일함

- 즉 마할라노비스 거리의 제곱은 타원이 됨



- Correlation Distance

- 데이터 간 Pearson correlation을 거리측도로 사용하는 방식으로, 데이터 패턴의 유사도를 반영할 수 있음
- Spearman Rank Correlation Distance

- ρ 를 Spearman correlation 이라 하며, 이는 데이터의 rank를 이용하여 correlation distance를 계산하는 방식임
- ρ의 범위는 -1 부터 1로, Pearson correlation과 동일

[참조] 김성범 교수님의 https://www.youtube.com/watch?v=W-DNu8nardo 를 요약한 것입니다.
'Machine Learning > Algorithm' 카테고리의 다른 글
| Ensemble learning (Stacking) (0) | 2020.05.06 |
|---|---|
| 모델 해석 기법 (Explainable) (0) | 2020.05.05 |
| 인공 신경망 (Neural Network) (0) | 2020.03.12 |
| Logistic regression (로지스틱 회귀모델) - 2 (학습, 해석) (0) | 2020.03.11 |
| Logistic regression (로지스틱 회귀모델) - 1 (배경, 형태, odds) (0) | 2020.03.05 |